八月 16

作者:
2016/8/16 下午 10:20 

當負載接上電源後，將從電壓引出電流，流過負載，然後返回電源，構成電流迴路，其所產生的電能S，負載消耗電能的快慢，稱為電功率，消耗越快表示所需的電能越大，亦即電流越大。

S = VRMS * IRMS

 

 

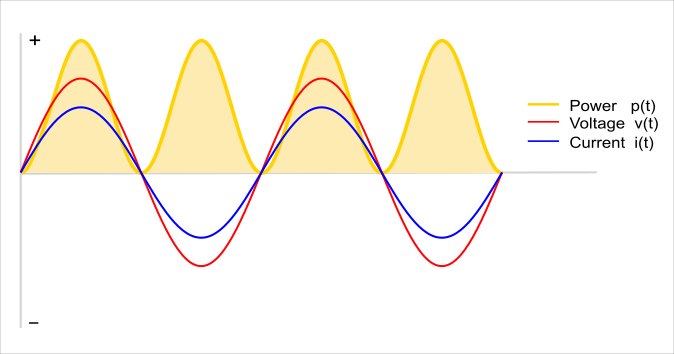
大部分的負載都是屬於電感性負載，例如冰箱，洗衣機，日光燈或馬達等，這些負載會吸收一定的能量，然後將一些能量釋放回電源。

 

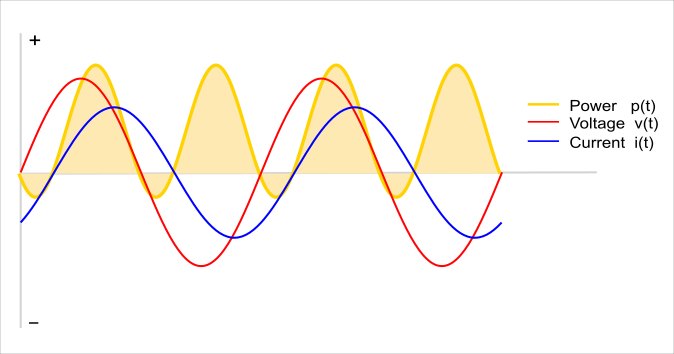
電感性負載其電流落後電壓

 

正值是從電源到負載的有效功率，流向負載的電能；負值是從負載返回到電源的無效功率，即負載流回的電能。

 

視在功率（電能），以複數表示，如等號左側；若以向量表示，如等號右側

 

S=P+j Q= √((P^2+Q^2 ) ) ∠θ θ=tan^(-1)⁡(Q/P)

 

其中S（視在功率）、P（有效功率，或稱負載消耗功率）、Q（無效功率，感抗或容抗所造成的損失）各個參數的單位依次為KVA、KW、KVAR，θ 為電感性負載的電流落後電壓的相位。

 

對於負載或用電設備其消耗電力之多寡，係設備實際消耗的功率以P（KW）來表示。

 

功率因數pf 定義為有效功率與視在功率的比值，介於0與1之間。負載的有效功率為定值，功率因數越大表示無效功率越小，反之則越大。

pf=P/S

 

功率三角形

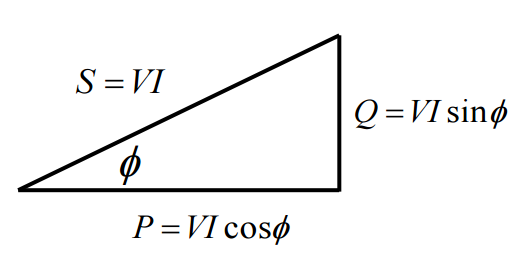
pf=P/S= (VI cos⁡θ)/VI= cos⁡〖θ θ=cos^(-1)⁡(pf) 〗

 

例如pf = 0.8，θ = cos-1（0.8）= 36.87o
 

---

某一負載之RＬ之等效串聯電路，電阻R = 40 Ω，電感 L = 0.2 H（Henry），電源為60 Hz 110 V，試求此負載之功率因數？

 

 

感抗 XL = ω * L = 2 * π * f * L = 2 * π * 60 * 0.2 = 75.4 Ω

總阻抗 Z = R + j XL = √（R2 + XL2）∠θ，其中θ = tan-1（XL / R）電阻R與感抗XL的向量夾角

 

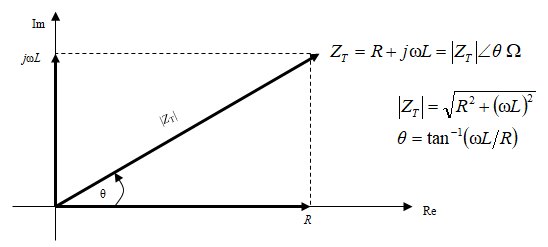
Z = 40 + j 75.4 = 85.35 ∠ 62.05o

電流 I = V / √（R2 + XL2）
I = 110 V / 85.35 Ω = 1.29 A

有效功率 P = I2 * R = 1.292 * 40 = 66.56 W
視在功率 S = V * I = 110 V * 1.29 A = 141.9 VA

功率因數 pf = P / S = 66.56 / 141.9 = 0.47
或 pf = cosθ = cos（62.05o）= 0.47 （同上）

無效功率 Q = √（S2 - P2）= √（141.92 – 66.562） = 125.32 VAR
Q = VI * sinθ = 141.9 * sin（62.05o） = 125.32 VAR（同上）

故此負載容量標示為耗電66.56 W，功率因數是0.47
電流 I = S / V =（P / pf）/ V = （66.56 W / 0.47）/ 110 V = 1.29 A （同上）
 

---

 

電感之電功率為無效功率，總電力消耗為零。

 

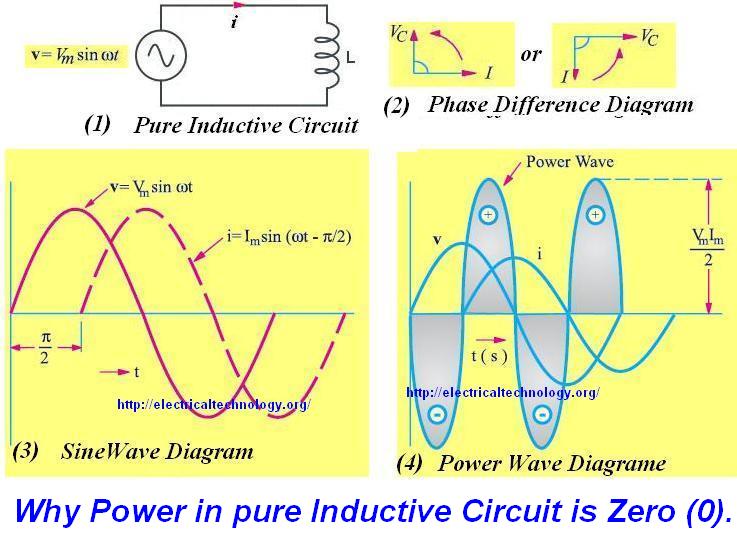
電感之電功率，p = v * i，如灰色曲線部分，當電流或電壓每變化一週（60 Hz），電功率已變化兩週，水平線以上的正半波可看成是將電能送往電感，儲存在磁場中，到了負半波在把電能釋放出來，送回電源，一個週期下來正負抵銷，總電力消耗為零

 

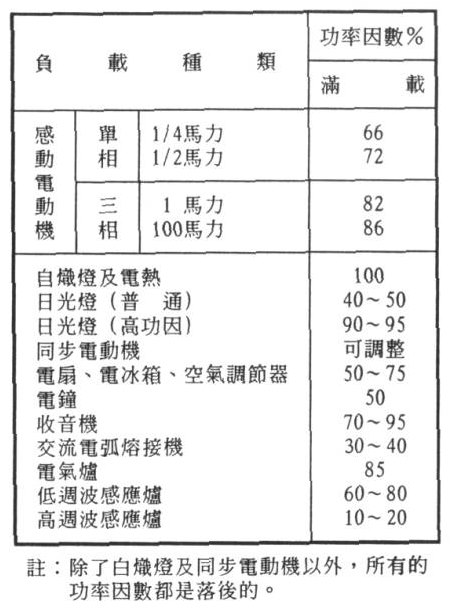
常見負載的功率因數